Variable neutral density (ND) filters are designed to allow variable light reduction from between 2-8 stops from a single filter. These filters are very flexible compared to fixed neutral density filters, but have a reputation of causing color casts and strange banding when used at their maximum densities with wide angle lenses. While inexpensive Vari-ND filters can be had for $30-40, the top of the line Singh-Ray are over $400.
So as part of the Photography Gear Lending Library program, I hired a Marumi Vari-ND filter to see what it could and couldn’t do. The Marumi is a mid- to high-end filter that retails for about US $125. It is made in Japan, and seems to be solid and well-constructed.
I first tested it for sharpness, as I’d read complaints about Vari-ND filters causing softness. I couldn’t detect any real softness in real life subjects.
Test Series #1 @17mm
I then tried it out with a moderate wide angle lens (17mm on a DX body) on a bright sunny day.
This series shows the results with no filter, then with the variable ND filter from its minimum to maximum setting. With the aperture at f/2.8 and metering for the sky, the shutter speed was 1/2500 without the filter. At its maximum density, the filter reduced the shutter speed down to 1/30, which is about 7 stops. I used Aperture priority, matrix metering and auto white balance. There are some subtle color shifts, but nothing more than I’m used to using a polarising filter. At the maximum setting there is a noticeable variation in the sky (the sun was to the left), but again, not really that different than what I’ve seen using a polarising filter against a wide expanse of sky.
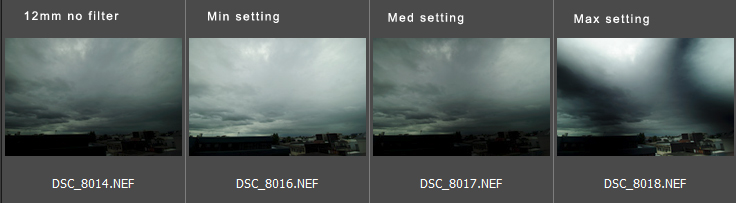
Test Series #2 @12mm
Next I tried the filter out with at 12mm, again on a DX body. This time against an overcast sky. Beyond about 4 stops the sky was not uniform at all, and by the max setting there was the dreaded cross effect that Vari ND filters are known for. At 18mm, I have not seen any sign of this strong cross effect. The main reason for seeing the effect I believe is the wider angle. The cloudy sky may contribute (although I doubt it).
And a real life image
Finally I used the filter in a real situation, photographing a nearby waterfall. It was a sunny day, mid-morning. The sun was mostly behind clouds, but without a filter I was metering about 1/400 at f/11 and ISO 200. With the filter, depending on the sunlight, I was able to take exposures of between f/9 and f/22 of 2-10 seconds. The nice thing about the variable ND filter was that you can set it to its minimum density, and quite easily focus and compose, then turn up the density to take the shot. At maximum density you almost can’t see anything in the viewfinder.
I took about 100 shots. There were a few that came out looking a bit blue, so I switched to Sunny white balance (instead of auto white balance) and had no further issues with color.
The below image was taken at f/9 and 3 seconds.
Summary
I had been wary of these Vari-ND filters, figuring they were too good to be true, unless possibly you shelled out $400 for the top of the line Sinh-Ray. I was pleasantly surprised with the performance of the Marumi. Compared to the hassle of Cokin style filter holders and stacking a number of ND filters, and the additional complication of trying to frame and focus without the filters in place, it is so much more convenient to just twist the vari filter ring and dial in whatever light reduction you need. They do have limitations at extremes (max density and ultra wide angle focal lengths), but in my opinion, these are good value.
Filed under PhotoSE Gear Grant



The link for the “Photography Gear Lending Library” gives a 404 error 🙁
I’ll fix that. Correct link is this: http://meta.photo.stackexchange.com/questions/2011/call-for-participants-in-photography-gear-lending-library
Thanks! This is great info. I thought about buying one at one time or another but now I know to avoid these things. The tests are quite telling.
The dreaded ‘cross’ or ‘butterfly’ effect comes when the two elements are not lined up properly. Sometimes that way from the factory, sometimes from repeated use. It’s not difficult to unscrew the retaining ring with a rubber stopper and rotate on element until the cross is gone at maximum ND.
Available here in Europe: http://www.camerafilterstore.nl/Marumi-DHG-Vari-ND-400-Grijsfilters.html